Mahir Salihbašić

Prenex normal forms in Wolfram Mathematica

This one caused me quite a pain while trying to find a way to check my work on rewriting first-order predicates in their prenex form, especially because it wasn’t actually documented in Mathematica (for whatever reason). I eventually stumbled upon a StackExchange thread which had the solution among its answers/comments.

In order for this to work, you’ll need to:

  1. Use Logical`Expand[predicate] to get a normal form predicate
  2. Use Reduce`ToPrenexForm[predicate] on the normal form to get the prenex normal form

Here is an example code returning a prenex normal form of the following formula:

(∀x)(F(x) ∧ (∃y)(G(y) ∧ H(x,y))) ⇒ (∃y)(T(y) ∧ P(a,b))

1
2
3
4
5
6
7

predicate = 
 Implies[ForAll[x, F[x] && Exists[y, G[y] && H[x, y]]], 
  Exists[y, T[y] && P[a, b]]]

normalForm = LogicalExpand[predicate]

prenexNormalForm = Reduce`ToPrenexForm[normalForm]

In Mathematica 13, it looks like this:

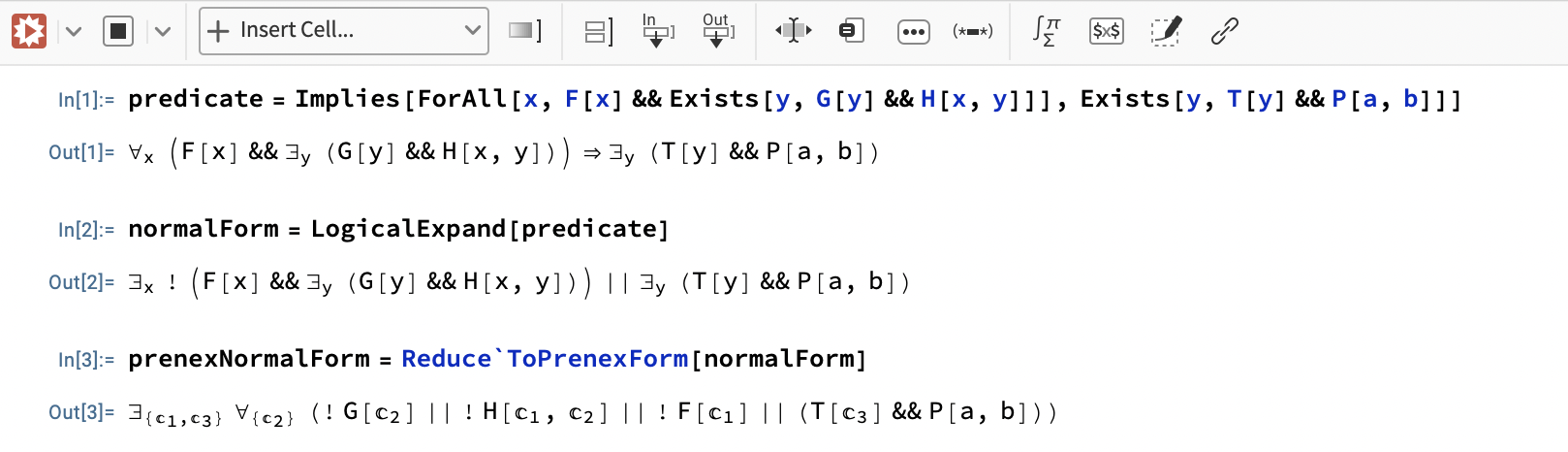
Above source code in Mathematica

Unfortunately, the output is a little bit clunky, with unintuitive variable names, but it seems like that can’t be helped. Still, it is perfectly fine for making sure moderately complex prenex normal forms are fine, after a lot of manual work, of course.